You are given a colored tree on $$$n$$$ nodes, node $$$i$$$ has color $$$c_i$$$. As a reminder, a tree on $$$n$$$ nodes is a connected graph with $$$n-1$$$ edges.
Compute the number of connected subgraphs of this tree, for which there exists some color (majority color), such that strictly more than half of the nodes of this subgraph have this color.
Since the answer can be quite large, compute it modulo $$$998\,244\,353$$$.
The first line of input contains one integer $$$n$$$ ($$$1 \le n \le 3000$$$) — the number of nodes in the tree.
The second line contains $$$n$$$ integers $$$c_1\ c_2\ \ldots\ c_n$$$ ($$$1 \le c_i \le n$$$) — the colors of the nodes.
The $$$i$$$-th of next $$$n-1$$$ lines contains $$$2$$$ integers $$$u_i, v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$), representing the edge $$$(u_i, v_i)$$$ of the tree. It is guaranteed that the given graph is a tree.
Print a single integer — answer to the problem modulo $$$998\,244\,353$$$.
3 2 3 3 1 2 2 3
5
4 1 1 3 3 1 2 1 3 1 4
8
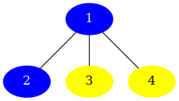
In the following pictures, we use blue for color $$$1$$$, red for color $$$2$$$, and yellow for color $$$3$$$. The first example looks as follows:

The tree has a total of $$$6$$$ non-empty connected subgraphs: $$$3$$$ of size $$$1$$$, $$$2$$$ of size $$$2$$$ and $$$1$$$ of size $$$3$$$, the latter in fact being the whole tree. All such subgraphs of sizes $$$1$$$ and $$$3$$$ have a majority color. For those of size $$$2$$$ only the subgraph induced by vertices $$$1$$$ and $$$2$$$ does not have a majority color (red and yellow both appear equally often in it). Therefore, there are $$$6 - 1 = 5$$$ connected subgraphs with a majority color.
The second example looks as follows, and it has $$$8$$$ connected subgraphs with a majority color:
| Name |
|---|




