Consider an undirected tree. The following algorithm constructs a post-order traversal of the tree:
fun dfs(v):
mark v as used
for u in neighbours(v):
if u is not used:
dfs(u)
append v to order
The post-order traversal will be in the list order.
You are allowed to choose the order of neighbors for each vertex as well as the starting vertex. What is the lexicographically minimal order you can get?
The first line of input contains one integer $$$T$$$ ($$$1 \le T \le 10^{5}$$$) — the number of test cases you need to process. Description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^{5}$$$) — the number of vertices in the tree.
The $$$i$$$-th of the next $$$n-1$$$ lines contains two integers $$$u_i, v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$), meaning that there is an undirected edge $$$(u_i, v_i)$$$ in the tree. It is guaranteed that the given graph is a tree.
The sum of $$$n$$$ over all test cases in one test file does not exceed $$$2 \cdot 10^{5}$$$.
For each test case print the lexicographically minimal order on a separate line.
3 3 1 3 3 2 3 2 1 1 3 7 1 2 1 3 2 4 2 5 3 6 3 7
1 2 3 2 1 3 4 5 2 1 6 3 7
The first test looks as follows:
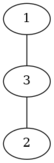
By starting in vertex $$$1$$$ we can only get order $$$2\ 3\ 1$$$. By starting in vertex $$$2$$$ we can only get order $$$1\ 3\ 2$$$. By starting in vertex $$$3$$$ we can get two orders: $$$1\ 2\ 3$$$ and $$$2\ 1\ 3$$$. The lexicographically minimal of the four orders is $$$1\ 2\ 3$$$.
The second test looks as follows:
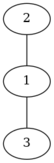
By starting in vertex $$$1$$$ we can get two orders: $$$2\ 3\ 1$$$ and $$$3\ 2\ 1$$$. By starting in vertex $$$2$$$ we can only get order $$$3\ 1\ 2$$$. By starting in vertex $$$3$$$ we can only get order $$$2\ 1\ 3$$$. The lexicographically minimal of the four orders is $$$2\ 1\ 3$$$.
The third test looks as follows:
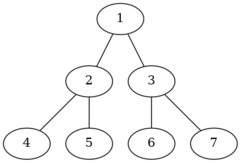
The lexicographically minimal order is $$$4\ 5\ 2\ 1\ 6\ 3\ 7$$$ it can be obtained by starting in node $$$7$$$.
| Name |
|---|




